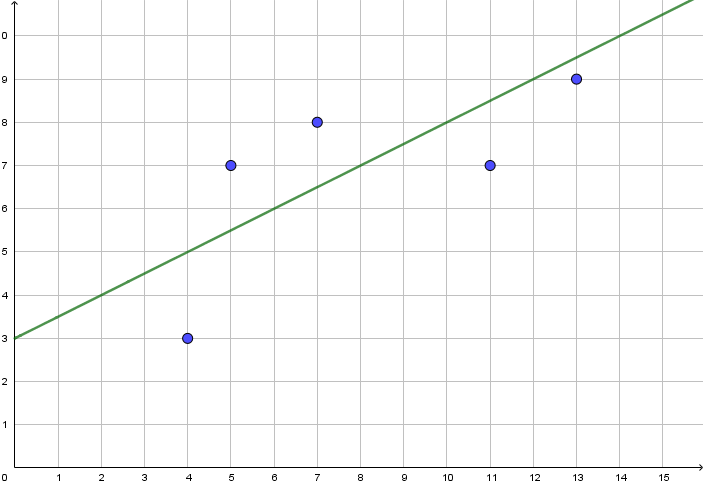
Quelle est l’équation de la droite (d1 ) et présente sur ce graphique ?
-> L’équation est de la forme y = ax+b
-> a est le coefficient directeur : a = 0,5
-> b est l’ordonnée à l’origine : b = 3
REPONSE
l’équation de la droite (d1) est y = 0,5x + 3
Donne les valeurs de chaque point placé sur ce repère.
Il faut mettre en premier les abscisses :
A(4;3) B(5;7) C(7;8) D(11;7) E(13;9)
Calculer les moyennes x̅ et y̅ , place le point G(x̅,y̅) sur ce graphique. Quel est ce point ?
| coordonnées | calcul moyenne | moyenne | |||||
|---|---|---|---|---|---|---|---|
| abscisse x | 4 | 5 | 7 | 11 | 13 | ( 4 + 5 + 7 + 11 + 13 ) ÷ 5 | = 8 |
| ordonnées y | 3 | 7 | 8 | 7 | 9 | ( 3 + 7 + 8 + 7 + 9 ) ÷ 5 | = 6,8 |
REPONSE
Les coordonnées du pont moyen sont G(8 ; 6,8)
Tracer les droites d’équation (d2 ) y=0,45x+4 et (d3 ) y=0,35x+4,5
Laquelle de ces 3 droites est celle qui passe le plus proche de tous les points ?
Il faut prendre la droite qui passe par le point moyen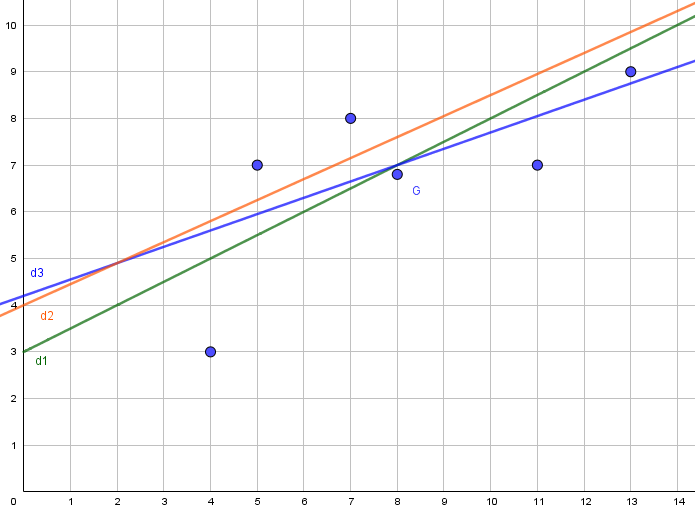
voir le graphique
-> Les droites les plus proches sont les droites d3 et d1.
-> En mesurant les écarts entre les points et la droite, celle qui s’en approche le plus est la droite d1