Premier degré

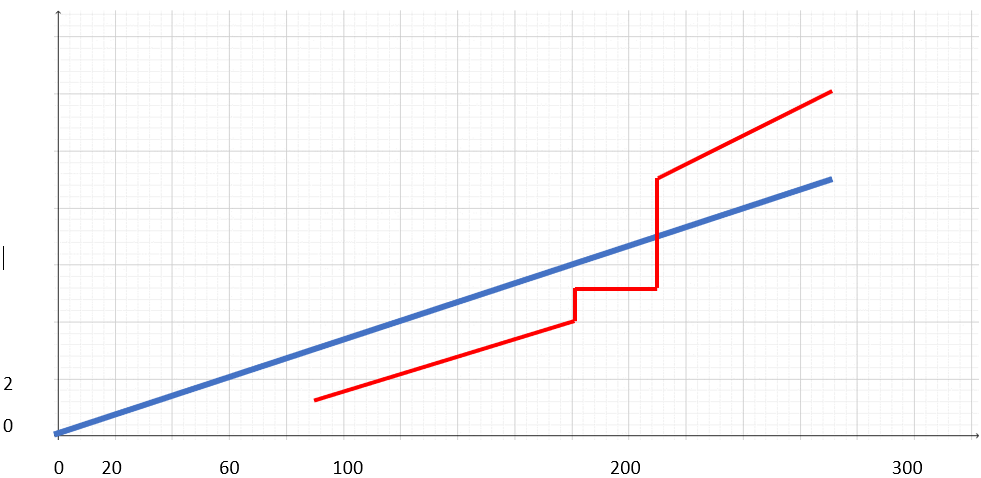
Une carte d’abonnement pour le cinéma coute 12€, qui permet d’avoir une entrée au tarif de 5€.
Paulo prétend avoir dépensé 77€ cette année pour le cinéma combien de film a-t-il vu ?
Propose une méthode de ton choix pour résoudre ce problème

Méthode 1 : compter :
> 1er place : 12+5 = 18€ ;
> 2eme : 18+5 = 22€ ;
> 3eme ..etc.. 13e : 77€

Méthode 2 soit x le nombre d’entrées
5x + 12 = 77 soit x= (77-12) ÷ 5 = 13

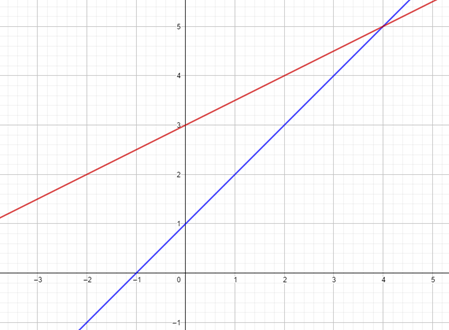
Deux agriculteurs possèdent des champs ayant un coté en commun de longueur inconnue. L’un est en forme de carré, l’autre en forme de triangle rectangle de base 100m.

Il faut utiliser les formules ci-dessous.
x×x=(100×x)/2
x(x-50)=0
x=0 ou x=50

Informations : aire d’un carré : côté×côté ; aire d’un triangle : (base × hauteur)/2

Règles:

Identifier ce qui est inconnu
Donner un nom simple à cette inconnue
Poser l’équation : traduire du français vers les mathématiques
Résoudre l’équation
Répondre en français

Exercice 1
Réduis l’expression quand c’est possible :
7×(-2x) | -3x-8x | 3x-5 | 3x×5

7×(-2x)= 7 × (-2) × x = -14x
-3x-8x= (-3 -8)×x = -11x
3x-5= 3x-5, on ne mélange pas
3x×5= 3×5×x = 15x

Exercice 2
Résoudre l’équation d’inconnue réelle x :
a) 2x + 1 = 3x–2

On peut tester avec 3
2×(3) + 1 = 7 (on remplace la variable « x » par le chiffre « 3 »)
et 3×(3) – 2 = 7
Les deux membres sont égaux, la solution est x = 3

b) 2x+1=3x+2

1 – 2 = 3x – 2x (on met les « x » d’un coté, les nombres de l’autre)
-1 = x (on calcule une fois que l’équation est équilibrée)
x = -1
-> il faut TESTER si x= -1 fonctionne

c) 8x-3=2x+5

6x = 8 (on a équilibré et on calcule)
x = 8/6
x = 4/3
-> il faut TESTER si x= 4÷3 fonctionne

Trace écrite :

✓ Une fois l’équation posée, il est possible de la résoudre : à la main ou à la calculatrice
✓ Il est possible de remplacer l’inconnue par certaines valeurs pour tester
✓ Il est interdit d’additionner les chiffres et les inconnues entre eux
✓ Il est possible de multiplie les chiffres et les inconnues entre eux

Timothée, 6 mois, a renversé son biberon alors qu’il a déjà bu 150 mL ! Comment reconstituer son biberon afin qu’il ait la bonne quantité préconisée pour son âge ?
Voici un tableau récapitulatif des quantités nécessaires pour réaliser un biberon pour un nourrisson.

Age (mois)	Quantité d’eau (mL)	Mesurettes de lait	Mesurettes de céréales	Mesurettes de soupe
1	90	3
2	120	4
3	150	5
4	180	6
5	180	6
6	210	7
7	210	7	3
8	210	7	3
9	210	7	3
10	240	8	4	5
12 et plus	270	9	5	6

Représenter en bleu sur ce repère le nombre de mesurettes de lait en fonction de la quantité d’eau.


voir le graphique

voir graphique

Sur ce même repère, représente en rouge l’âge du bébé en fonction de la quantité d’eau.

Quelle droite est une situation de proportionnalité ? Donner le coefficient multiplicateur.

La droite bleue car c’est une droite qui passe par l’origine. Le coefficient multiplicateur est 1÷30                             

En déduire graphiquement la réponse à la problématique.

Il faut 210mL, il en manque 210-150 = 60mL
60mL correspond à 2 mesurettes de lait. Il faut faire 60mL d’eau avec 2 mesurettes de lait         

Trouve l’équation qui permet de connaitre le nombre de mesurettes en fonction de la quantité d’eau.

30mL d’eau correspond à une mesurette. C’est une situation de proportionnalité
Nombre de mesurettes = quantité d’eau ÷ 30    

Une équation avec une inconnue se représente graphiquement
Il peut y avoir des situations de proportionnalité (b=0)
Les valeurs peuvent être saisies dans un tableau
Il est possible de passer du tableau au graphique

NB : se produit lorsque la représentation graphique est une droite qui passe par l’origine

Soit le parallélogramme représenté ci-dessous. Les cotes sont en mm.

2) Calcule le périmètre lorsque

3) Si son périmètre est de 42 cm, déterminer x.

4) On cherche à obtenir un tableau de valeurs et la représentation graphique des valeurs possibles de ce périmètre.

Interprétation des résultats obtenus par la calculatrice

4a) D’après le tableau de valeurs, quelle est la valeur du périmètre pour x=2 ? Que remarque-t-on ?

On retrouve le résultat de la question

4b) Combien mesure le périmètre pour x= 5 ?

A l’aide du tableau, on trouve 22mm

4c) Quelle est la valeur de   pour obtenir un périmètre de 102cm ?

Pour x = 25