La France a accueilli du 30 novembre au 11 décembre 2015 la Conférence Paris Climat (COP 21). Ce fut une échéance cruciale, puisqu’elle devait aboutir à un nouvel accord international sur le climat, applicable à tous les pays, dans l’objectif de maintenir le réchauffement climatique mondial en deçà de 2°C. En effet, le cinquième et dernier rapport du GIEC, publié en 2013, souligne l’importance des activités humaines dans le dérèglement climatique et ses principales manifestations :
- La température moyenne annuelle a déjà augmenté de 0,85 °C depuis 1880 et pourrait croître jusqu’à près de 5°C d’ici à 2100 ;
- Plus de 90% de l’énergie due au réchauffement climatique est stockée dans l’océan ;
- L’océan Arctique pourrait être libre de glace avant le milieu du 21e siècle et les glaciers de montagne continueront à se vider. Le niveau de la mer s’est élevé de 0,19 mètre au cours de la période 1901-2010. Le GIEC prévoit une hausse probable de 26 à 89 cm entre 2010 et 2100 ;
- Les concentrations de CO2 liées à l’homme ont augmenté de 40% depuis 1750 et de 20% depuis 1958.
Source : d’après cop21.gouv.fr
Document ressource : repère
→Le tableau ci-dessous donne l’évolution du niveau moyen global des océans, estimé à partir des données marégraphiques d’une ville côtière
| Année | 1900 | 1910 | 1930 | 1940 | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
| Niveau de la mer (mm) | 198 | 235 | 239 | 302 | 343 | 364 | 378 | 402 | 429 | 431 |
→ Les prévisions du GIEC sur l’augmentation du niveau de la mer entre 2010 et 2100 sont-elles envisageables?
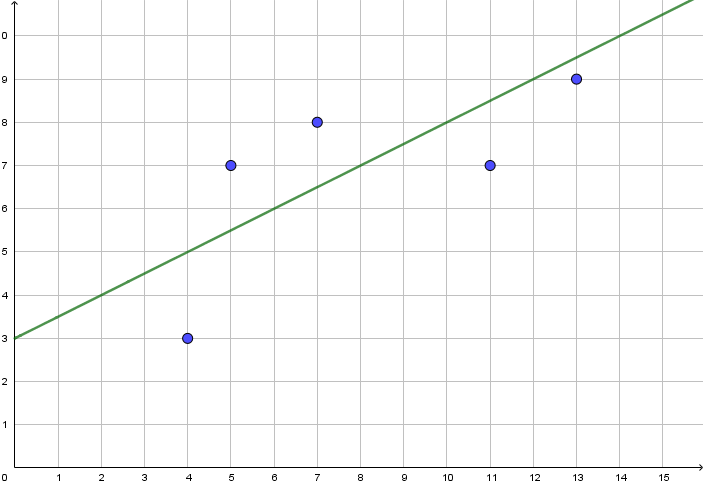
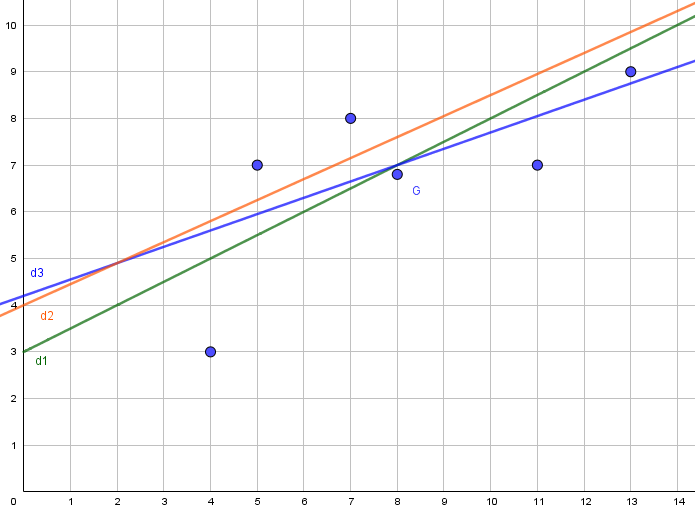
Il faut tracer sur un graphique les points, et imaginer vers la direction que prennent ces points.
Sur l’axe des abscisse (horizontal), on prendra les années, et sur les ordonnées (axe vertical), la hauteur en mm. Nous encadrerons approximativement ce nuage de points par deux droites pour estimer le niveau de la mer en 2100.
Construction de l’échelle:
En abscisse (horizontal)
-> la valeur minimale est l’année 1900,
-> la valeur maximale en abscisse est 2100 (et non 2010). Dans la question il est demandé une valeur pour l’année 2100.
En ordonnée :
-> la valeur minimale est 198mm.
-> la valeur maximale est 431mm + 89cm (prévision la plus pessimiste du GIEC) soit 1320mm .
==>Nous pouvons prendre 190 et 1300 pour avoir des valeur facile à placer.
Pour estimer la hauteur en 2100 :
Encadrer par deux droites le nuage de points (droites bleues). On trouve deux valeurs en 2010 : 640 et 665 mm (avec les droites noires puis violettes).
REPONSE:
On peut estimer que le niveau global des océans sera compris entre 640 et 665mm. Cette estimation est cohérente, elle se siture dans la fourchette basse des prévisions du GIEC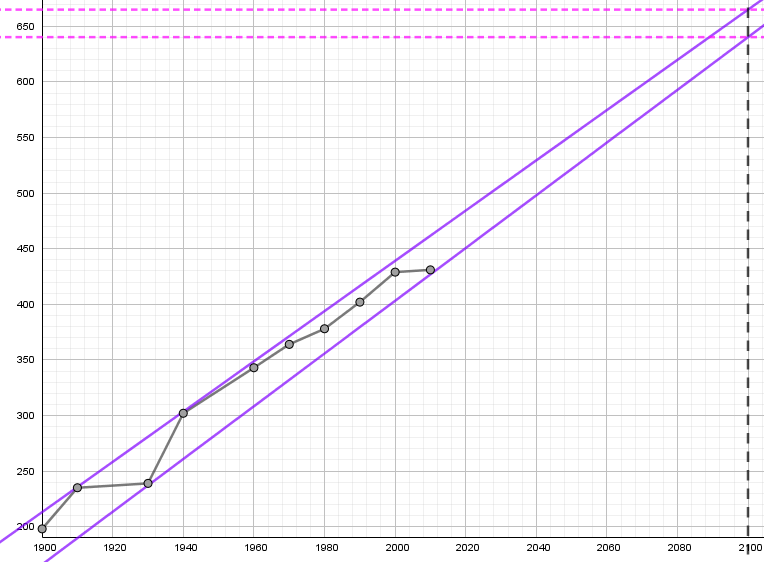
voir graphique réponse ici
| Année | 1970 | 1980 | 1990 | 1995 | 2000 | 2005 | 2010 | 2015 |
| Température (°C) | 13,98 | 14,23 | 14,31 | 14,39 | 14,69 | 14,83 | 14,96 | 15,22 |
> En 1880, la température moyenne était d’environ 13,8 °C. En l’absence d’accord et de mesures efficaces, en quelle année la température moyenne deviendrait-elle supérieure de 2 °C à cette valeur?
Il faut également positionner les points sur un graphique. On peut utiliser le même graphique avec deux échelles en ordonnées (axe vertical). Bien comprendre que la valeur minimale peut être 13,98°C et le maximum : 13,8 + 2°C = 15.8°C.
On peut construire l’échelle en partant de 13 à 16 pour graduer facilement le repère.
Il faut cette fois-ci partir d’une valeur en degré (axe des ordonnées) pour lire un intervalle sur l’axe des années (axe horizontal). En suivant la ligne noire puis les lignes violettes, nous estimons que :
REPONSE
La température aura augmenté de 2°C entre 2035 et 2046. Cette estimation est soumis à la position des droites qui encadrent le nuage de points.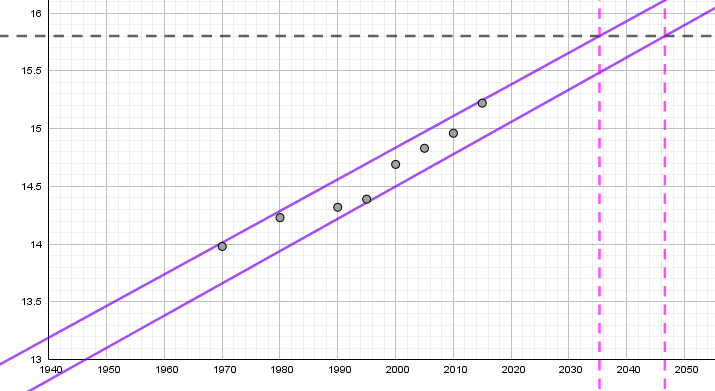
voir le graphique